Aflevering 10: Krachtsluiting

Het vormsluiten van de lading is al beschreven in aflevering 8 is al behandeld. Laten we nu de wrijvingsverbinding eens nader bekijken. Wat wordt bedoeld met hechting, hoe werkt het en wat is belangrijk bij het vastzetten van ladingen?

Definitie van

Een wrijvingsverbinding is een verbinding van twee delen via het oppervlak, waarbij beide oppervlakken een hoge wrijvingscoëfficiënt hebben. Hoe werkt het?

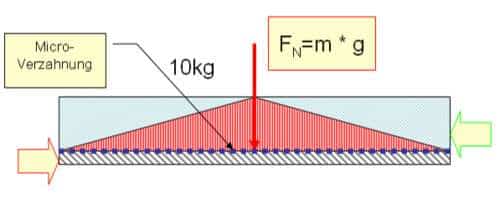
Een last drukt op een oppervlak met een aangenomen gewicht van 10 kg. De normaalkracht wordt berekend door de massa (voorbeeld 10 kg) te vermenigvuldigen met de zwaartekracht g (9,81 ^m/s2).

De normaalkracht is dus 10 kg * 9,81 m/s2⁼ 100 N.

De normaalkracht werkt altijd verticaal op het oppervlak.

Elk oppervlak heeft een bepaalde ruwheid, waardoor een microvertanding ontstaat wanneer de twee oppervlakken met elkaar in contact komen. De afmeting wordt aangegeven met de letter µ en wordt de wrijvingscoëfficiënt genoemd.

Als nu wordt geprobeerd de oppervlakken tegen elkaar te bewegen, creëert deze ruwheid een tegenkracht. Het is precies dit effect dat wordt gebruikt bij krachtsluiting .

De tegenkracht hangt af van de specifieke wrijvingscoëfficiënt µ en wordt de wrijvingskracht genoemd.

Als een fabrikant van vrachtwagencarrosserieën bijvoorbeeld een wrijvingscoëfficiënt van µ=0,3 opgeeft voor zijn laadoppervlakken, betekent dit dat de kracht die nodig is om pallets te verplaatsen 30% van de normaalkracht is.

Krachtsluitende ladingbeveiliging

Hoe werkt de krachtgesloten borging van een vrijstaande last van 1000 kg tegen verplaatsing tijdens voluit remmen met 0,8 g? (zie VDI-2700 en EN-12195-1).

De vereiste borgkracht volgens de voorschriften is
_FS = m * g * a = 1.000 kg * 9,81 ^m/s2 * 0,8 g = 8.000 N = 800 daN

Een lading wordt meestal vastgesjord met spanbanden. De kracht die nu de verplaatsing tegenwerkt bestaat nu uit twee componenten: de normaalkracht + de voorspankracht.

Er moet echter rekening worden gehouden met de invloed van drie randvoorwaarden:

• de wrijvingskracht_FR uit de wrijvingscoëfficiënt µ
• de sjorhoek α tussen het bevestigingspunt en het 1e afbuigpunt
• de overdrachtscoëfficiënt/K-factor tussen de twee bevestigingspunten

De wrijvingskracht

De voorspankracht kan ook worden gezien als een extra gewicht aan de lading. Dit betekent dat alleen het deel van de voorspankracht dat overeenkomt met de wrijvingscoëfficiënt effectief is.

Wrijvingskracht_FR = 1.000 daN * 0,3 = 300 daN
Borgkracht FS = 500 daN * 0,3 = 150 daN
Totaal: 450daN

Er is dus een kracht van slechts 450 daN nodig om 1.000 kg te verplaatsen.

Het voorbeeld laat zien dat de voorspankracht van 500 daN niet voldoende is om de belasting tegen verschuiven te beschermen. maatregelen zoals vastsjorren.

De sjorhoek

Een andere randvoorwaarde voor de grootte van de effectieve voorspankracht is de sjorhoek α, omdat alleen het verticale deel van de voorspankracht effectief is. De verhouding is het resultaat van de sinus van de sjorhoek.

Voorbeeld: met een sjorhoek α van 80º is de sinus 0,9961.

Dit betekent dat slechts 500 daN * 0,9961 = 498 daN van de voorspankracht van 500 daN daadwerkelijk effectief is.

De transmissiecoëfficiënt

De voorspanning die door de spanratel wordt gegenereerd, bestaat alleen tussen het bevestigingspunt op de laadvloer en het 1e doorbuigpunt. Het wordt verminderd op de afbuigpunten door wrijvingsverliezen. Hoe meer afbuigpunten, hoe groter het verlies.

De som van de voorspankracht bestaat daarom uit minstens drie delen:

• Deel 1: Bevestigingspunt – afbuigpunt 1
• Deel 2: Afbuigpunt 1 en 2
• Deel 3: Afbuigpunt 2 – Bevestigingspunt

Het resultaat kan worden berekend met behulp van de transmissiecoëfficiënt/K-factor. Uitgaande van een factor 1,5 zou de som van de voorspankracht 500 daN * 1,5 = 750 daN zijn.

Aantal spangordels

Als nu alle randvoorwaarden samen worden bekeken volgens het voorbeeld, resulteert de volgende berekening:

_FSTF = voorspankracht * K-factor * sin sjorhoek α * µ
= 500 daN * 1,5 * sin35º (0,5735) * 0,3 = 129 daN

Hoeveel spanbanden zijn er nodig om deze lading vast te zetten? Hierbij kan de volgende overweging worden gemaakt:

800 daN moet worden vastgezet, als je hiervan de wrijvingskracht van 450 daN aftrekt, levert dat een verschil van 350 daN op. Deze kracht moet worden geleverd door spanriemen . 350 daN gedeeld / 129 daN = 2,7 wat betekent dat er 3 spanbanden nodig zijn om de lading van 1.000 kg vast te zetten onder de gespecificeerde randvoorwaarden.

De conclusie is beangstigend, want van 500 daN, wat op zich veel is, is er eigenlijk maar heel weinig over. Hieruit kan worden geconcludeerd dat de bevestigingsmethode met wrijvingsvergrendeling voor het vastzetten van spanbanden aan veel beperkingen onderhevig is en daarom met de grootst mogelijke voorzichtigheid moet worden gebruikt.

Een algemene oplossing is de combinatie van spanbanden + antislipmatten met µ=0,6.

Het verhogen van de wrijvingscoëfficiënt is het doorslaggevende element.

Wrijvingskracht_FR = 1.000 daN * 0,6 = 600 daN
Voorspankracht _FSTF = 500 daN * 1,5 * sin35º (0,5735) * 0,6 = 258 daN
Borgkracht_FS = 600 daN + 258 daN = 858 daN

Vastzetbalans: de werkelijke vastzetkracht moet gelijk zijn aan of groter zijn dan de vereiste vastzetkracht. 858 daN ≥ 800 daN

In de praktijk zie je vaak precies het tegenovergestelde. Vermoedelijk door een gebrek aan kennis van het principe van actie.

Hoogachtend, Sigurd Ehringer

Tobias Kreft