Folge 21: Stausack Ladungssicherung – Teil 2

Warum gibt es in den meisten Fällen keine Probleme, obwohl kaum jemand die Mathematik bemüht?

Das lässt sich anhand von Berechnungen nachweisen. Unter der Voraussetzung dass, wie in Teil 1 beschrieben, keine handwerklichen Fehler gemacht werden.

Als Grundsatz gilt: Die Sicherungskraft durch das Polster muss mindestens genauso groß sein, wie die Kraft, welche aus der Ladung entsteht, und die Ladung darf sich nicht bewegen.

Fallbeispiele

Was würden diese Fasspaletten wohl bei einem Rollwinkel von 37º tun?

Sie würden natürlich rutschen oder kippen. Eine Rollperiode von bis zu 2-3 mal pro Minute ist nicht ungewöhnlich. Der Rollwinkel 38º würde der maximalen Beschleunigung von 0,8 g quer zur Fahrtrichtung entsprechen.

Nehmen wir als Beispiel den klassischen Fünferblock aus Europaletten, wie er in Teil 1 beschrieben wurde.

Die Ladeeinheiten wiegen jeweils 900 kg und sind 1,60 m hoch. Die Seitenlänge der beiden Blöcke beträgt jeweils 2,40 m.

Die Frage ist nun, wie groß muss das Staupolster sein, damit die Kraft aus der Ladung mit 80% Polsterfläche kompensiert wird.

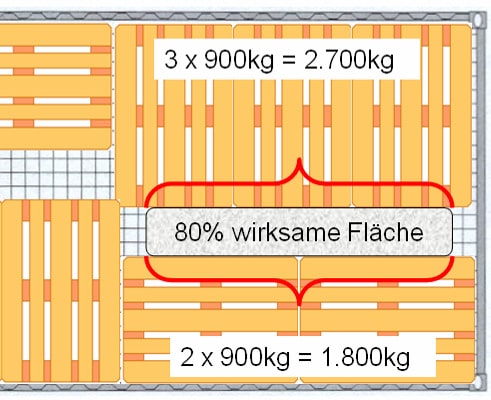
Polsterfläche errechnen:

Seitenlänge:
2,40 m x 0,8 = 1,92 m

Höhe:
1,60 m x 0,8 = 1,28 m

Lückenbreite:
0,34 m

Die Breite der Lücke zwischen den Ladeeinheiten ergibt sich aus der Innenbreite des Containers von 2,34 m, abzüglich der Palettenmaße 1,20 m + 0,80 m, also 0,34 m.

Formel für die wirksame Fläche eines Staupolsters

Schritt 1

In der Formel ist sowohl die Breite (b_DB) als auch die Höhe (h_DB) und die Lückenbreite (d) enthalten.

Um das jeweilige Ausgangsmaß ermitteln zu können, müssen die Elemente der Formel umgestellt werden:

Aus (b_DB – π * d/2) wird (b_DB + π * d/2) und aus (h_DB – π * d/2) wird (h_DB + π * d/2)

Schritt 2

Im nächsten Schritt ist die zulässige Belastung des Polsters der Kraft aus der Ladung gegenüber zu stellen. Es muss mindestens ein Gleichgewicht herrschen.

Der CTU-Code gibt für die Polsterbelastung folgende Formel vor:

Mit den Werten aus dem vorstehenden Beispiel ergibt sich: F_DB = 1,92 * 1,28 * 10 * 9,81m/s2 * 0,55 * 0,75 [kN] = 67,77 kN.

Die Kraft, welche dieses Polster einer Ladung entgegensetzen kann beträgt also 6.777 daN.

Schritt 3

Der weitere Schritt ist die Berechnung der Kraft, welche sich aus der Ladung ergibt.

Hier die Formeln aus dem CTU-Code für eine gleitende/kippende Ladung. Es ist jedoch besonders zu beachten, dass das Gewicht in Tonnen und nicht wie gewohnt in Kilogramm angegeben wird.

Die Werte aus dem Beispiel in die Berechnung eingesetzt ergibt folgendes:

F_Ladung = 2,7 to * 9,81 m/s2 * (0,8 – 0,3 * 0,75 * 0,2) [kN]
F_Ladung = 26,45 * (0,8 – 0,045) [kN]
F_Ladung = 26,45 * 0,755 = 19,97 kN = 1.997 daN

Die Sicherungskraft (6.777 daN), welche sich aus dem Staupolster ergibt, ist also um das 3,3 fache größer als die Kraft (1.997 daN), welche sich aus der  Ladung ergibt.

Das bedeutet im Umkehrschluss, wenn die Polstergröße so gewählt wird, dass die Ladung flächig gehalten wird, also weder kippen, rutschen, noch sich  drehen kann, ist die Sicherungskraft des Polsters im Regelfall immer ausreichend.

Ihr Sigurd Ehringer

Sigurd Ehringer

✔ VDI-zertifizierter Ausbilder für Ladungssicherung ✔ Fachbuch-Autor ✔ 8 Jahre Projektmanager ✔ 12 Jahre bei der Bundeswehr (Kompaniechef) ✔ 20 Jahre Vertriebserfahrung ✔ seit 1996 Berater/Ausbilder in der Logistik ✔ 44 Jahre Ausbilder/Trainer in verschiedenen Bereichen —> In einer Reihe von Fachbeiträgen aus der Praxis, zu Themen rund um den Container und LKW, erhalten Sie Profiwissen aus erster Hand. Wie sichert man Ladung korrekt und was sind die Grundlagen der Ladungssicherung? Erarbeitet und vorgestellt werden sie von Sigurd Ehringer, Inhaber von SE-LogCon.