
Now 10% off all Ergolash lashing straps save now! Voucher code: ergo10 | Valid until 31.05.2025
Why are there no problems in most cases, even though hardly anyone does the math?
This can be proven on the basis of calculations. Provided that, as described in Part 1, no technical errors are made.

As a basic principle, the securing force exerted by the pad must be at least as great as the force exerted by the load, and the load must not move.
What would these barrel pallets do at a rolling angle of 37º?
They would naturally slip or tip over. A rolling period of up to 2-3 times per minute is not unusual. The roll angle of 38º would correspond to the maximum acceleration of 0.8 g transverse to the direction of travel.

Let’s take the classic block of five Euro pallets as an example, as described in Part 1.
The load units weigh 900 kg each and are 1.60 m high. The side length of the two blocks is 2.40 m each.
The question now is, how large must the dunnage bag be so that the force from the load is compensated by 80% of the cushioning area?
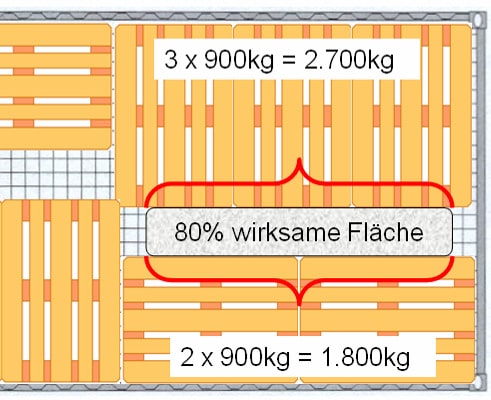
Calculate the upholstery area:
Side length:
2.40 m x 0.8 = 1.92 m
Height:
1.60 m x 0.8 = 1.28 m
Gap width:
0.34 m
The width of the gap between the loading units results from the internal width of the container of 2.34 m, minus the pallet dimensions of 1.20 m + 0.80 m, i.e. 0.34 m.
The formula from the CTU code for the effective area of the cushion is as follows:
A = (bDB – π * d/2) * (hDB – π * d/2)
The formula contains the width (bDB) as well as the height (hDB) and the gap width (d).
In order to determine the respective initial dimension, the elements of the formula must be rearranged:
(bDB – π * d/2) becomes (bDB + π * d/2) and (hDB – π * d/2) becomes (hDB + π * d/2)
To stay with the example described, the production dimensions for the upholstery result from the following calculation:
Length/width = (bDB + π * d/2) = 1.92m + 3.14 * 0.34/2) = 1.92m + 0.53m = 2.45m
Upholstery height = (hDB + π * d/2) = 1.28m + 3.14 * 0.34/2) = 1.28m + 0.53m = 1.81m.
The next step is to compare the permissible load on the pad with the force from the load. There must be at least a balance.
The CTU code specifies the following formula for the pad load:
FDB = A * 10 * g *PB * SF [kN]
Using the values from the example above, the result is: FDB = 1.92 * 1.28 * 10 * 9.81m/s2 * 0.55 * 0.75 [kN] = 67.77 kN.
The force that this cushion can exert against a load is therefore 6,777 daN.
The next step is to calculate the force resulting from the load.
Here are the formulas from the CTU code for a sliding/tilting load. However, it is important to note that the weight is given in tons and not in kilograms as usual.
Sliding:
FLADUNG = m * g * (cx,y – μstatic * 0.75 * cz ) [kN]
Tilting:
FLADUNG = m * g * (cx,y – bp /hp * cz ) [kN]
Inserting the values from the example into the calculation results in the following:
LOAD = 2.7 to * 9.81 m/s2 * (0.8 – 0.3 * 0.75 * 0.2) [kN]
LOAD = 26.45 * (0.8 – 0.045) [kN]
LOAD = 26.45 * 0.755 = 19.97 kN = 1,997 daN
The securing force (6,777 daN) resulting from the dunnage bag is therefore 3.3 times greater than the force (1,997 daN) resulting from the load.
Conversely, this means that if the size of the cushion is selected so that the load is held flat, i.e. cannot tip, slide or turn, the securing force of the cushion is generally always sufficient.
Yours, Sigurd Ehringer
<< Previous article
Episode 20: dunnage bag Load securing – Part 1
Next post >>
Episode 22: Floor loads on trucks

Sigurd Ehringer
✔ VDI-zertifizierter Ausbilder für Ladungssicherung ✔ Fachbuch-Autor ✔ 8 Jahre Projektmanager ✔ 12 Jahre bei der Bundeswehr (Kompaniechef) ✔ 20 Jahre Vertriebserfahrung ✔ seit 1996 Berater/Ausbilder in der Logistik ✔ 44 Jahre Ausbilder/Trainer in verschiedenen Bereichen —> In einer Reihe von Fachbeiträgen aus der Praxis, zu Themen rund um den Container und LKW, erhalten Sie Profiwissen aus erster Hand. Wie sichert man Ladung korrekt und was sind die Grundlagen der Ladungssicherung? Erarbeitet und vorgestellt werden sie von Sigurd Ehringer, Inhaber von SE-LogCon.
Rothschenk assortment
Our customer center has only one goal: to turn your problems into solutions. Whether standard stowage cushions, bestsellers or load securing personally tailored to your needs -. we accompany you consistently from A as in field service to Z as in certification. That is our promise to you, as a leader in our industry.
We attach great importance to professional cargo securing. That is why we have our own production, which ensures reliable operation through modern manufacturing technologies and strict quality control. Thus, we offer our customers a comprehensive and high-quality range of services in the field of transport logistics.
DIN ISO 9001:2015, EMAS and Ecovadis are not foreign words to you? Then it's time to work with the best.
You don't take any risks with us - we have been awarded the Platinum Medal on the EcoVadis sustainability rating platform.
As a load securement company, we are proud to have several certifications that validate our sustainability efforts and our commitment to environmental protection and social responsibility. For you as a purchaser, this means that we demand and promote the implementation of high environmental and social standards both within the company and along the supply chain.
G&H GmbH Rothschenk
Industriestrasse 5 & 7-10
97239 Aub
Phone: +49 9335 97 15 – 79
Fax: +49 9335 97 15 – 15
E-mail: info@rothschenk.de
Collection/delivery
Mon – Fri: 8:00 – 15:00
Office hours
Mon – Thu: 8:00 – 17:00
Fri: 8:00 – 13:00
G&H GmbH Rothschenk
Industriestrasse 5 & 7-10
97239 Aub
Phone: +49 9335 97 15 – 0
Fax: +49 9335 97 15 – 15
E-mail: info@rothschenk.de
Collection/delivery
Mon – Fri: 8:00 – 15:00
Office hours
Mon – Thu: 8:00 – 17:00
Fri: 8:00 – 13:00
You are currently viewing a placeholder content from Google Maps. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information